The Koch Snowflake is a neat fractal shape… that you can make in your kitchen.

Some time ago we showed how you can make Sierpinski triangles out of polymer clay, and followed that up by making fractal cookies, in the pattern of the Sierpinski carpet.
Another well-known simple fractal is the Koch Snowflake– soon to be known as the Koch Cupcake! For this project we are experimenting with making iterated fractals out of edible doughs: marzipan and rolled fondant. We should note up front that neither is particularly easy to work with in this level of detail, but the result may well be worth the effort. Koch Cupcakes (along with Sierpinski cookies) certainly rank as optimal geek chow.
While the Koch Snowflake is a beautiful shape, it is not necessarily obvious how to go about constructing it physically.

The algorithm to do this was demonstrated by Instructables member LarrySDonald, who showed how to do this same project last year (with less edible clay).

The first thing to recognize about building it is that it consists of three identical Koch curves placed around a triangular core. That gives us a simplification: we can first make the Koch curve by iteration, and then cut it into thirds and place it around the core.

Let’s look a detailed look at the algorithm:

We begin (1) by making a triangular cane of (in this case) blue fondant. That’s “iteration 0” in the usual terms that are used to describe this shape. We then stretch that cane until it’s it has one ninth the cross-sectional area, and (2) cut it into four pieces. We then (3) assemble those four pieces together with a similarly sized triangular cane of white fondant. Finally (4) we add a triangular cap of blue fondant. This last part is not strictly necessary as part of the iteration process to produce the shape on a computer, but is done to produce a final triangular shape that can be easily worked by hand in the next iteration.

In the next iteration, we begin (1) with the output material from the first iteration– a blue triangular cane with a smaller white triangle inset.
Again we stretch that (2) into four smaller pieces and assemble them (3) with a piece of fresh white material. Note the orientation of the triangles in this step. To continue iterating, we again apply a triangular cap.

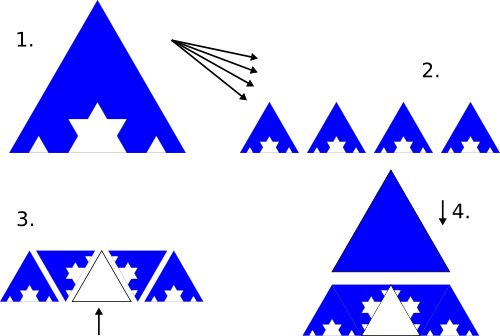
Iteration 3 is produced the same way, and you can continue iterating with the same process until the limit of your patience– or at least for the case of edible doughs, until they begin to dry out too much.

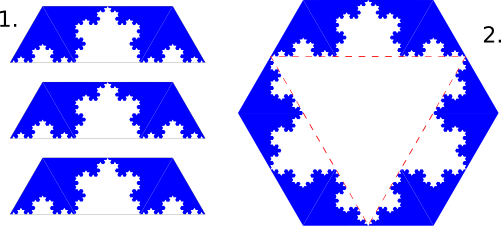
After the last iteration that will be performed, you can leave off the triangular cap, and instead (1) cut the resulting cane into three pieces, which are then (2) placed around a larger triangular cane of white material, finally realizing the snowflake shape.

We began our physical construction with Wilton rolled fondant. It comes in a box, ready made. We split a large chunk into two pieces. One piece we left as white material. The other piece we colored blue with gel food coloring, which adds less moisture to the fondant than regular food coloring does. Also note: rubber gloves are a good idea when working with concentrated food coloring!

After rolling out and stacking the triangular canes, here is iteration number 1.

And iteration number 2.

We did three iterations (fondant is fickle) and assembled the final snowflake out of narrow slices, rather than building a giant cane of it. We put the parts down on the cutting board and rolled them together, creating a smooth shape on the underside.

Just add cupcakes….

As we mentioned earlier, we also tried marzipan.

   a>

Marzipan comes in a tube. It works into a nice flexible dough and it’s quite tasty. It has the same sort of drying problems that fondant does, and the natural color is that of almonds rather than that of sugar. It can also be colored with the application of gel food coloring.

And there we have it: Koch Cupcakes in fondant and marzipan.
As we have mentioned before, the interesting thing about fractals like these is that they are emergent phenomena– complex patterns that show up when a simple algorithm is iterated. We often think of mathematical iteration as something that only happens in computers, but as these examples show, there are a number of interesting certain cases where you can perform iteration with your hands as well.